Grundlagen der Heiligen Geometrie
Einige Grundlagen und zentralen Begriffe der heiligen Geometrie
Der Goldene Schnitt
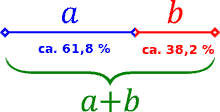
Der Goldene Schnitt ist ein bestimmtes Verhältnis zweier Grössen zueinander – zum Beispiel der Länge zweier Strecken. Zwei Strecken stehen im Verhältnis des Goldenen Schnittes, wenn sich die größere zur kleineren Strecke verhält, wie die Summe aus beiden zu der grösseren.
Der Begriff Goldener Schnitt wurde erst ab der ersten Hälfte des 19. Jahrhunderts populär, obwohl die mathematischen Prinzipien schon seit der Antike bekannt waren.
1202 kommt der italienische Mathematiker Leonardo da Pisa, genannt „Fibonacci“, kurz auch auf die später nach ihm benannten Fibonacci-Folge zu sprechen, und zwar im Zusammenhang mit der sogenannten Kaninchen-Aufgabe, in der zu errechnen ist, wie viele Kaninchenpaare bei einer Fortpflanzungsrate von einem Paar Jungkaninchen pro Elternpaar und Monat nach Ablauf eines Jahres insgesamt vorhanden sind, wenn ein erstes Paar bereits im ersten Monat und dessen Nachwuchs jeweils ab seinem zweiten Lebensmonat Junge wirft. Leonardo führt die Zahlenfolge für jeden Monat vor (2, 3, 5, 8 … bis 377) und weist darauf hin, dass sich jedes Glied der Reihe (ab dem dritten) durch Summierung der beiden vorhergehenden Reihenglieder errechnen lässt.
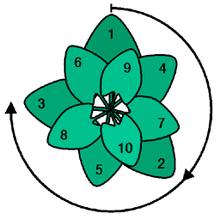
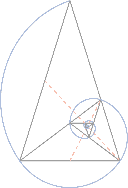
In der Natur kommen viele so genannte Fibonacci-Spiralen vor, deren Aufbau sich aus dieser Zahlenreihe ableitet. Das spektakulärste Beispiel für Verhältnisse des Goldenen Schnittes findet sich bei der Anordnung von Blättern (Phyllotaxis) und in Blütenständen mancher Pflanzen. Bei diesen Pflanzen teilt der Winkel zwischen zwei aufeinander folgenden Blättern den Vollkreis von 360° im Verhältnis des Goldenen Schnittes, wenn man die beiden Blattansätze durch eine Parallelverschiebung eines der Blätter entlang der Pflanzenachse zur Deckung bringt. Es handelt sich dabei um den Goldenen Winkel von etwa 137,5°.
Die daraus entstehenden Strukturen werden auch als selbstähnlich bezeichnet: Auf diese Weise findet sich ein Muster einer tieferen Strukturebene in höheren Ebenen wieder. Beispiele sind die Sonnenblume, Kohlarten, Kiefernnadeln an jungen Ästen, Zapfen, Agaven, viele Palmen- und Yuccaarten und die Blütenblätter der Rose, um nur einige zu nennen.
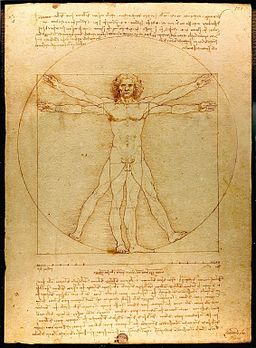
Der Goldene Schnitt findet sich auch im menschlichen Körper – fast alle unsere Gelenke beispielweise teilen die Gliedmassen annähernd im Verhältnis des goldenen Schnitts. Und auf die Gesamtlänge des Körpers bezogen, befindet sich auch der Bauchnabel grob im Goldenen Schnitt. Bekannt sind diese Körperverhältnisse spätestens seit Leonaro Da Vinci’s Bild des Menschen, der sowohl das Pentagramm als auch den Kreis und das Quadrat vereint:
Der goldene Schnitt ist die einzige Proportion, in der das Ganze sich im Verhältnis der Teile zueinander wiederspiegelt. “Wie dort oben, so hier unten” “Wie im Großen, so im Kleinen” Der Goldene Schnitt verdeutlicht auf materieller Ebene diese geistigen Gesetzmässigkeiten.
Vielleicht wird der Goldenen Schnitt deshalb von den Menschen als besonders ästhetisch empfunden und findet daher in Kunst und Architektur vielfältige Anwendung.
Die platonischen Körper
Die platonischen Körper sind die 5 geometrischen Körper, die durch regelmässige, untereinander kongruente Vielecke begrenzt werden. Ihre Namen stammen aus dem Griechischen und beziehen sich auf die Anzahl ihrer Flächen:
Tetraeder (Vierflächner aus vier Dreiecken),
Hexaeder (Sechsflächner bzw. Würfel aus sechs Quadraten),
Oktaeder (Achtflächner aus acht Dreiecken),
Dodekaeder (Zwölfflächner aus zwölf Fünfecken)
und Ikosaeder (Zwanzigflächner aus zwanzig Dreiecken).
Dualität
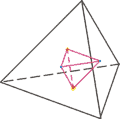
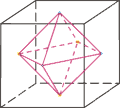
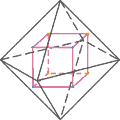
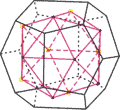
Zu jedem konvexen Polyeder lässt sich ein sogenannter Dualkörper konstruieren. Dessen Kanten konstruiert man, indem man die Mittelpunkte jeweils benachbarter Seitenflächen des Polyeders miteinander verbindet.
Somit hat das duale Polyeder genauso viele Ecken, wie das Ausgangspolyeder Flächen hat. Der Dualkörper hat zudem genauso viele Flächen, wie der Ausgangskörper Ecken hat. Letzteres kann man sich räumlich so vorstellen, dass jede („vergrößerte“) Fläche des Dualkörpers eine Ecke des Ausgangskörper abschneidet. Drittens gilt, dass das Dualpolyeder und sein Ausgangspolyeder die gleiche Anzahl an Kanten haben. Dies lässt sich ebenfalls aus obiger Konstruktion ablesen: Zwei „benachbarte Seitenflächen“ bilden gemeinsam eine Kante des Ausgangspolyeders, und die „Verbindung der zwei Mittelpunkte“ dieser benachbarten Seitenflächen stellt eine Kante des Dualkörpers dar.
Bei den Platonischen Körpern, als Untergruppe der konvexen Polyeder, gibt es bezüglich deren Dualkörper noch folgende Besonderheiten: Erstens haben hier Ausgangs- und Dualkörper denselben geometrischen Schwerpunkt. Zweitens ist der Dualköper eines Platonischen Körpers auch selbst ein Platonischer Körper. Dabei bilden Hexaeder (Würfel) und Oktaeder sowie Dodekaeder und Ikosaeder jeweils ein duales Paar. Das Tetraeder ist zu sich selbst dual, wobei sich jedoch das duale Tetraeder in (verkleinerter) zentralsymmetrischer Lage befindet, d. h., es „steht auf dem Kopf“. Drittens: Wiederholt man obige Konstruktion und konstruiert den dualen Körper zum Dualkörper, so erhält man einen „verkleinerten“ Ausgangskörper – also einen Platonischen Körper, der durch Zentrische Streckung in den Ausgangskörper überführt werden kann. Beide haben somit denselben Schwerpunkt.
Die platonischen Körper haben noch eine Besonderheit: Verbindet man die Mittelpunkte benachbarter Seitenflächen eines platonischen Körpers, so erhält man (mit den Verbindungslinien als Kanten) wieder einen platonischen Körper, und zwar mit demselben Mittelpunkt. Dieser Körper wird als Dualkörper zum Ausgangskörper bezeichnet.
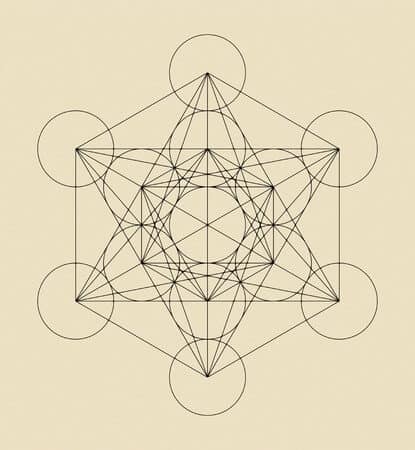
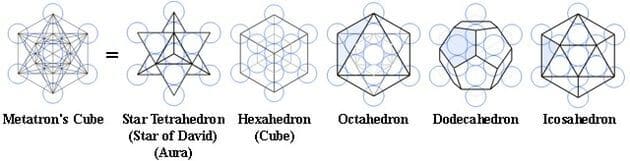
Verbindet man alle platonischen Körper zu einer Figur, erhält man den sogenannten Würfel Metatrons:
In diesem Gebilde sind alle anderen Körper enthalten:
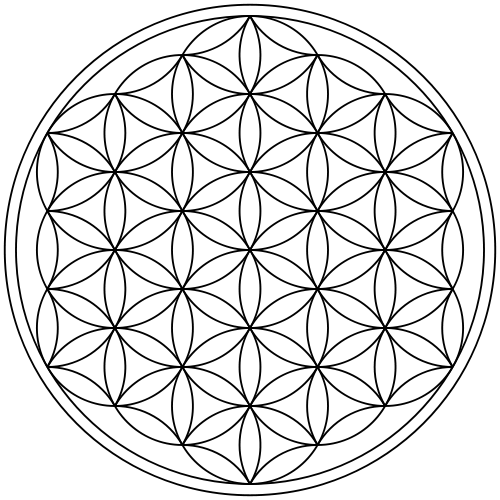
Blume des Lebens / Same des Lebens
Bereits die obigen platonischen Körper beinhalten die Kreise, aus denen sich die Blume des Lebens definieren lässt. Nähere Infos und Herleitung in den Büchern von Drunvalo Melchizedek – denn besser kann es hier nicht gesagt werden.
Die Blume des Lebens ist eine Struktur, die aus einer Vielzahl von Kreisen besteht, deren Mittelpunkte jeweils auf den Kreislinen der sechs umgebenden Kreise liegen.
Das Symbol (und daraus entnommene „Unterformen“, welche wiederum eigene Symbole darstellen) findet sich überall auf der Welt – in den Pyramiden in Ägypten, Mexiko und Peru, in Kirchen in ganz Europa, über Indien bis nach China und Japan.
Hier die Blume des Lebens von Leonardo Da Vinci.
Weitere Info dazu hier:
Andreas Beutel,Leiter der Pythagoras Institutes in Dresden: Höhere Ordnung – Blume des Lebens
Andreas Beutel,Leiter der Pythagoras Institutes in Dresden: Nichts geschieht zufällig – Die natürliche Ordnung im Universum